Set Theory Questions
A set is a well-defined collection of objects, known as elements or members of the set. Sets are usually denoted by capital letters & elements are usually denoted by small letters. If ‘a’ is an element of a set A, then we write a ϵ A (a belongs to A) otherwise a ∉A (a doesn’t belong to A).
Representation of sets: In mathematics, sets are commonly used to represent collections or groups of objects or elements. A set is defined as a well-defined collection of distinct element that are considered a single entity. These elements can be anything, such as numbers, letters, or even other sets.
1. Tabular or Roster form → In this form, elements are listed within the pair of brackets { } and are separated by commas.
e.g.— N = {1, 2, 3, 4 ….} is a set of natural numbers
2. Set-builder or Rule form: In this form, a set is described by a property that its member must satisfy.
e.g. — A = {x : x is natural number less than 10}
3. Statement form: In this representation, a well-defined description of the elements of the set is given.
e.g. — The set of all even numbers less than 10.
Different Types of Sets: In mathematics, sets can be classified into different types based on their properties and characteristics. Here are some commonly recognized types of sets
1. Null set → A set which does not contain any element is called a null set or an empty set or a void set.
2. Singleton set → A set which contains only one element.
3. Finite set → A set is called a finite set, if it is either void or its elements can be counted
The number of distinct elements of a finite set A is called the cardinal number & it is denoted by n(A).
4. Infinite set → A set which has an unlimited number of elements is called an infinite set.
5. Equivalence sets: Two finite sets A and B are equivalent if their cardinal numbers are the same.
6. Equal sets: Two sets are said to be equal if both have the same elements.
Note:– Equal sets are equivalent but equivalent sets may or may not be equal.
7. Subset: If every element of set A is an element of set B, then A is called a subset of B sit is denoted by A ⊆ B.
8. Superset → If set B contains all elements of set A, then B is called superset of A & it is denoted by B ⊇ A.
9. Proper subset → A set A is said to be a proper subset of set B, if A is a subset of B & A is not equal to B. It is denoted by A ⊂ B.
10. Universal set → Universal set is a set which contains all objects, including itself. It is denoted by U.
11. Power set → The set of all the possible subsets of A is called the power set & is denoted by P (A).
Note:-
1. The total number of subsets of a finite set containing n elements is 2ⁿ.
2. The total number of proper subsets of a finite set containing n elements is (2ⁿ –1).
3. If a set A has n elements, then its power set will contain 2ⁿ elements.
Operations on sets: In mathematics, various operations can be performed on sets to manipulate and combine them. These operations allow for the creation of new sets based on the relationships between existing sets. Here are the common operations on sets
1. Union of two sets: The union of two sets A and B is the set of elements which are in A, in B or in both A & B. The union of A & B is denoted by A ∪ B.
2. Intersection of two sets: The intersection of A & B is the set of all those elements which belong to both A & B & is denoted by A ∩ B.
3. Disjoint of two sets: Two sets A & B are said to be disjoint if they don’t have any common element (i.e. A ∩ B = ϕ).
4. Difference of two sets: The difference of sets A & B is the set of all those elements of A which do not belong to B. & is denoted by (A – B) or A\B.
5. Symmetric difference of two sets : The symmetric difference of sets A & B is the set (A – B) ∪ (B – A) and is denoted by A ∆ B.
6. Complement of a set: The complement of a set A is the set of all those elements which are in universal set but not in A. It is denoted by A^1 or A^C or U – A.
Laws of Algebra of sets: The laws of algebra of sets, also known as set identities or set laws, are a set of principles that describe the relationships and properties of sets. These laws help in manipulating and simplifying set expressions. Here are the fundamental laws of algebra of sets
1. (a) A ⊆ A ⋁ A
(b) ϕ ⊆ A ⋁ A
(c) A ⊆ U, ⋁ A in ∪
(d) A = B ⇔ A ⊆ B, B ⊆ A.
2. Idempotent laws:
(a) A ∪ A = A
(b) A ∩ A = A
3. Identity laws:
(a) A∪ ϕ = A
(b) A∩ ϕ = ϕ
(c) A ∩ U = A
(d) A ∪ U = U
4. Commutative law
(a) A ∪B = B ∪A
(b)A ∩B = B ∩ A
5. Associative laws
(a) (A ∪B) ∪C = A ∪ (B ∪ C)
(b) (A∩ (B ∩ C) = (A ∩ B) ∩ C
6. Distributive law
(a) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
(b) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
7. De-Morgan’s law
(a) (A∪B)^’ = A^’ ∩ B^’
(b) (A∩B)^’ = A^’∪B^’
8. (a) A – (B ∪C) = (A – B) ∩ (A – C)
(b) A – (B ∩ C) = (A – B) ∪ (A – C)
(c) A – B = A ∩ B^’ = B^’– A^’
(d) A – (A – B) = A ∩ B
(e) A – B = B – A ⇔ A = B
(f) A ∪B = A ∩ B ⇔ A = B
(g) A ∪A^’ = U
(h) A ∩ A^’ = ϕ
Important results:
1. n(A ∪ B)= n(A) + n(B) – n(A ∩ B)
2. n(A – B) = n(A) – n (A ∩ B)
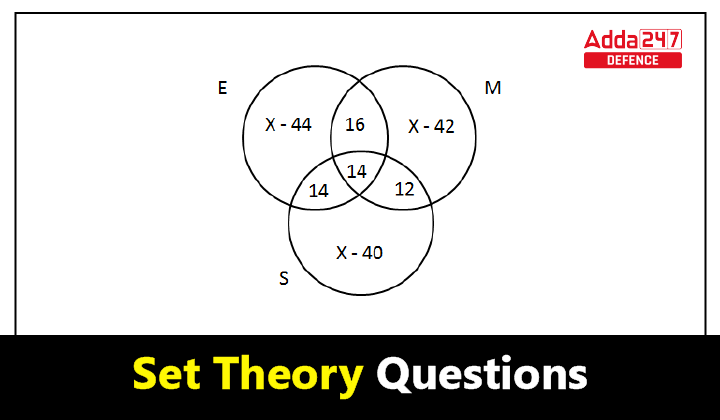
3. n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
4. n(A^’ ∪ B^’) = n ( A ∩ B)’ = n (U) – n(A ∩ B)
5. n(A^’∩ B^’) = n(A ∪ B)’ = n(U) – n(A ∪ B).
6. n (A ∆ B) = n (A) + n(B) – 2n(A ∩ B).
7. n(A’) = n(U) – n(A).
8. n(A ∩ B’) = n(A) – n(A ∩ B).
Set Theory Questions: Solved Examples
Here are a few solved examples of set theory questions:
1. The number of proper subsets of the set {1, 2, 4, 6} is:
Sol. Number of proper subsets of the set {1, 2, 4, 6} = 2⁴– 1 = 16 – 1 = 15.
2. In a group of 500 students, there are 475 students who can speak Hindi and 200 can speak English. What is the number of students who can speak Hindi only?
Sol. n(H) = 475, n(E) = 200, n (H ∪ E) = 500
n(H ∩ E) = n (H) + n(E) – n(H∪ E)
= 475 + 200 – 500 = 175.
Number of students who can speak Hindi only
= n(H) – n(H∩ E)
= 475 – 175 = 300
3. Let n(U) = 800, n(A) = 250, n(B) = 300, n(A∩B) = 350 then n(A’ ∩ B’) is equal to
Sol. n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
= 250 + 300 – 350
= 200
n(A’ ∩ B’) = n(A ∪ B)’ = n(U) – n(A ∪B)
= 800 – 200
= 600
4. Let U = {x ϵ N: 1 ≤ x ≤ 8} be the universal set, N being the set of natural numbers. If A = {1, 2, 3, 4} and B = {2, 4, 6, 8}. Then what is the complement of (A – B)?
Sol. A = {1, 2, 3, 4) B = {2, 4, 6, 8)
(A – B) = {1, 3}
(A – B)’ = U – (A – B)
= {1, 2, 3, 4, 5, 6, 7, 8} – {1, 3}
= {2, 4, 5, 6, 7, 8}


 List of Static GK (General Knowledge) Fo...
List of Static GK (General Knowledge) Fo...
 List of Dams and Reservoirs in India, Ch...
List of Dams and Reservoirs in India, Ch...
 List of the Important Mountain Passes of...
List of the Important Mountain Passes of...










